
If provided, the optional argument weight should be a 1D Tensor It is useful when training a classification problem with C classes. This criterion computes the cross entropy loss between input logits CrossEntropyLoss ( weight = None, size_average = None, ignore_index = - 100, reduce = None, reduction = 'mean', label_smoothing = 0.0 ) ¶ Extending torch.func with autograd.FunctionĬrossEntropyLoss ¶ class torch.nn.CPU threading and TorchScript inference.CUDA Automatic Mixed Precision examples.I hope this article has given a simple primer on decision trees, entropy, and information gain. Furthermore, we have shown this through a few lines of code. We have also mentioned the basic steps to build a decision tree. We have learned how decision trees split their nodes and how they determine the quality of their splits. Wrapping upĭecision trees are one of the simplest machine learning algorithms to not only understand but also implement. Remember to play around with the values of max_depth and min_samples_leaf to see how they change the resulting tree. subplots(figsize =( 6, 6)) #figsize value changes the size of plot tree. #max_depth represents max level allowed in each tree, min_samples_leaf minumum samples storable in leaf node #fit the tree to iris dataset clf. DecisionTreeClassifier(criterion = 'entropy', max_depth = 4,min_samples_leaf = 4) The minimum sample count storable in a leaf node.

Each decision tree has a maximum number of levels permitted. However, since we are building as simple a decision tree as possible, these two parameters are the ones we use. Let’s begin!įor trees of greater complexity, you should expect to come across more parameters. Our goal is to visualize a decision tree through a simple Python example. Repeat iteratively until you finish constructing the whole tree. From the image below, it is attribute A.īuild child nodes for every value of attribute A.

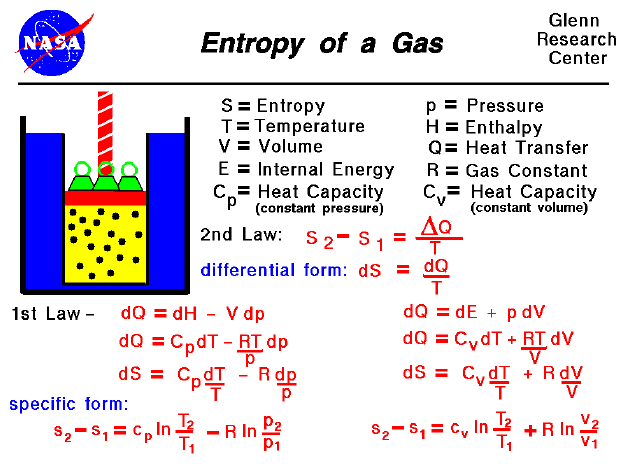
The higher the information gain, the better the split. The more the entropy removed, the greater the information gain. We can now get our information gain, which is the entropy we “lost” after splitting. After splitting, the current value is $ 0.39 $. The entropy may be calculated using the formula below: The image below gives a better description of the purity of a set.Ĭonsider a dataset with N classes. It determines how a decision tree chooses to split data.
#Entropy formula code#
A code editor such as VS Code which is the code editor I used for this tutorial.To follow along with the code, you’ll require: If you are unfamiliar with decision trees, I recommend you read this article first for an introduction. Steps to use information gain to build a decision tree
In this article, we will learn how information gain is computed, and how it is used to train decision trees. There are metrics used to train decision trees. Simply put, it takes the form of a tree with branches representing the potential answers to a given question. A decision tree is a supervised learning algorithm used for both classification and regression problems.


 0 kommentar(er)
0 kommentar(er)
